Re: Measuring the surgical ‘learning curve’: methods, variables and competency
Sir,
Khan et al. [1] present a new review of the use of learning curves (LCs) in clinical practice. It is enlightening to see how many confounding factors are involved when constructing a LC. Could LCs eventually provide a supplement to or even replace indicative numbers charting the progress of surgical trainees?
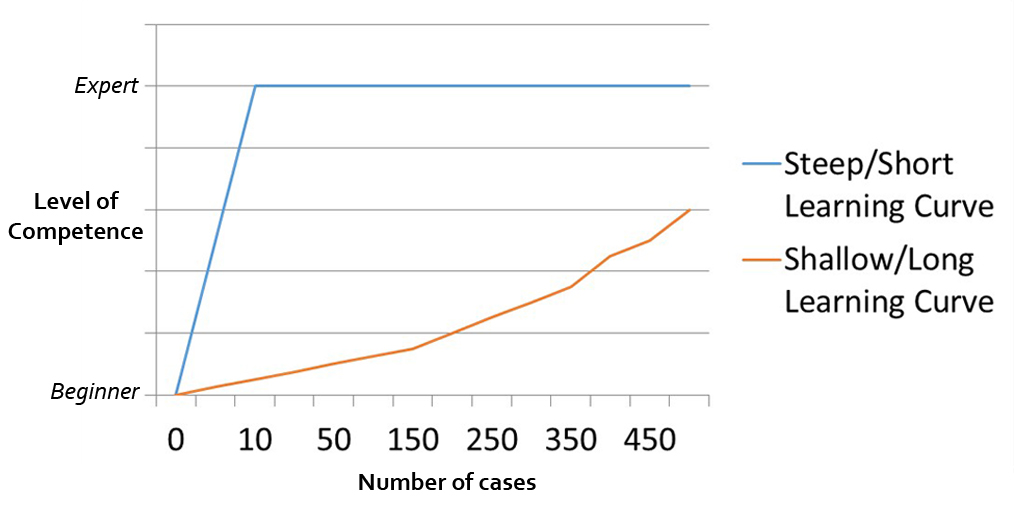
When considering using a LC to demonstrate competence in surgical training, the many measurable factors associated with skill acquisition are different for different procedures, as is the rate at which these skills are attained.
For some, large gains in expertise may be achieved with few simple procedures, producing a short or steep LC. The attainment of competence for a more complex procedure may require much more exposure, a shallow or long LC. The curve described by Khan et al. this month is only one way to learn. Pictured below are differing learning curves.
In addition, some operations lend themselves to an easier assessment of competence than others. Time versus resected, enucleated or vaporized tissue can be plotted for TURP and laser prostatectomy LC, with the efficiency of operator movement a surrogate for surgical expertise.
A LC may be punctuated by several plateaus as surgeons take on more complex cases, or through changes in the frequency and number of cases carried out over a specified period. The levelling out of an individual’s LC may provide an indication that progress has slowed. This would afford trainers to step in and facilitate further skill acquisition through other training means, such as simulation training or individual mentoring.
Or maybe, we have to consider that a learning curve, in fact, develops as outlined in this image from the Incentive Intelligence website?
Hannah Wells, Paul Sturch, Gordon Muir
Urology Department, King’s College Hospital, London, UK
Reference
- Khan N, Abboudi H, Khan MS, Dasgupta P and Ahmed K. Measuring the surgical ‘learning curve’: methods, variables and competency. BJU Int 2014; 113: 504–508